Visualizing Sorting Algorithms

🗓️ March 10, 2020 | 🕒 9 min read

In this post I’ll discuss some basic sorting algorithms: insertion, bubble and selection sort. Although inefficient, these are some of the easiest sorting algorithms to understand and are a great starting point to kick off a discussion about sorting.

Insertion sort #

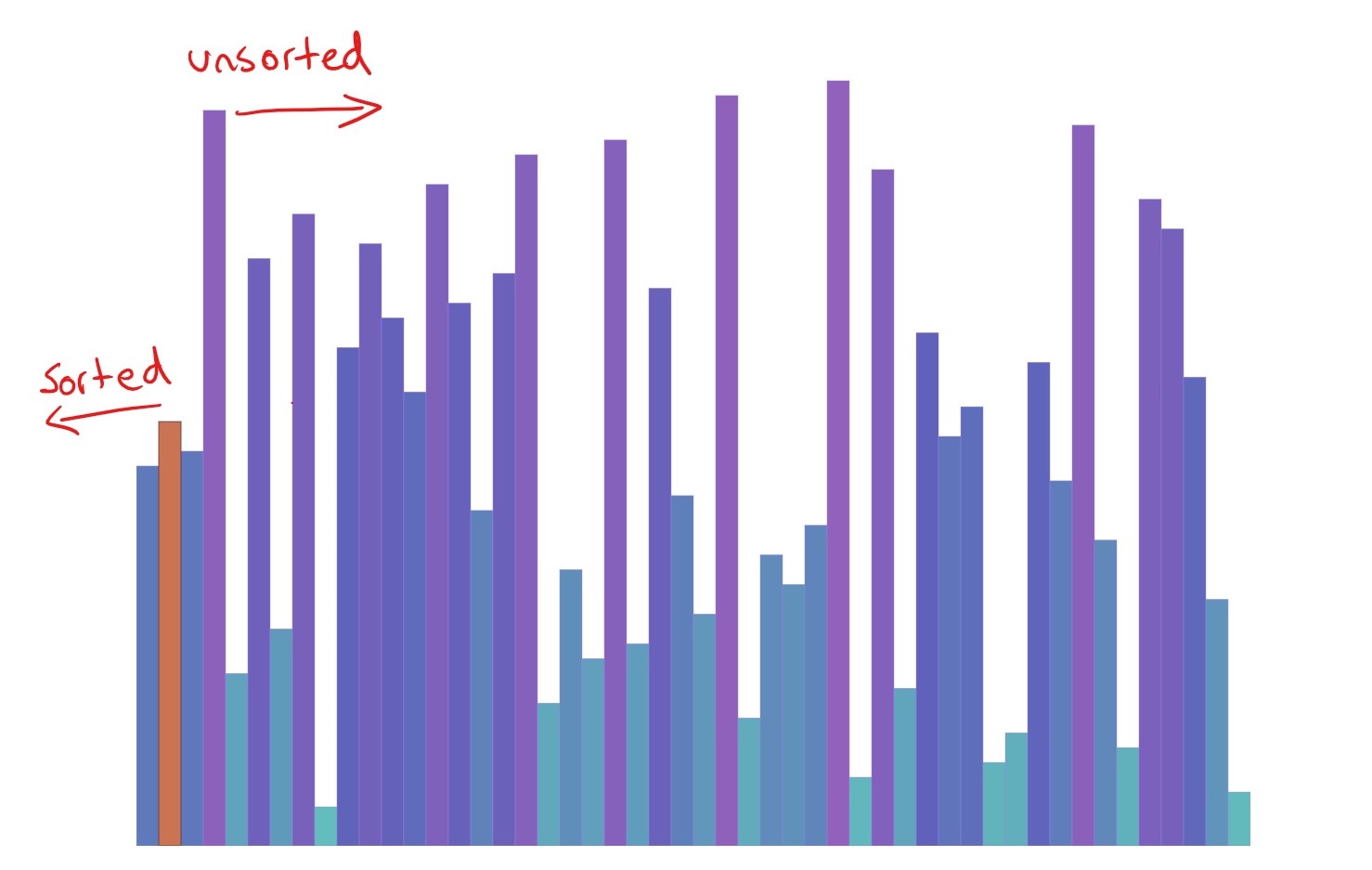
The basic principle of insertion sort is that as we move through our array, we sort it. Placing each value we encounter into its rightful position. As we move to the left of our array, we know that whatever is to the right is sorted (because we put it there).

Take a look at the visualisation. You can see the sorted array emerging. Slow down the frame rate or reduce the amount being sorted if you’re having trouble seeing it.

This visualisation implements the following code:

    function insertionSort(arr) {
        for (let i = 1; i < arr.length; i++) {
            let focusValue = arr[i];
            let j = i - 1;
            while (j >= 0 && arr[j] > focusValue) {
                arr[j + 1] = arr[j];
                arr[j] = focusValue;
                j = j - 1;
            }
        }
        return arr;
    }

In the animation, the orange bar is highlighting i and the yellow highlights j. The i is responsible for moving through the array, while the j is each value we are comparing i to. If we find that j points to a bigger value than i, we know that i belongs before it, so we need to shift the j value to the left by one and put the i value in its place.

We continue shifting values until the j value is no longer bigger than the focus value at i. Essentially, we are pushing the i value back into the sorted array until it ends up where it belongs.

The concept of knowing that everything behind i is sorted is a principle more formally known as a loop invariant.

The loop invariant #

Loop invariants are a tool used to help us understand an algorithm and reason why it is correct. It is a conditional statement that we know is correct before, during and after the loop runs. For example, for insertion sort, our loop invariant is the fact that everything before our pointer is sorted.

To fulfil all the requirements of being a loop variant, our condition must be true at all phases of the loop. That is before, during and after the loop runs. So lets double check that we can in fact use this reasoning for insertion sort…

Nothing sorted
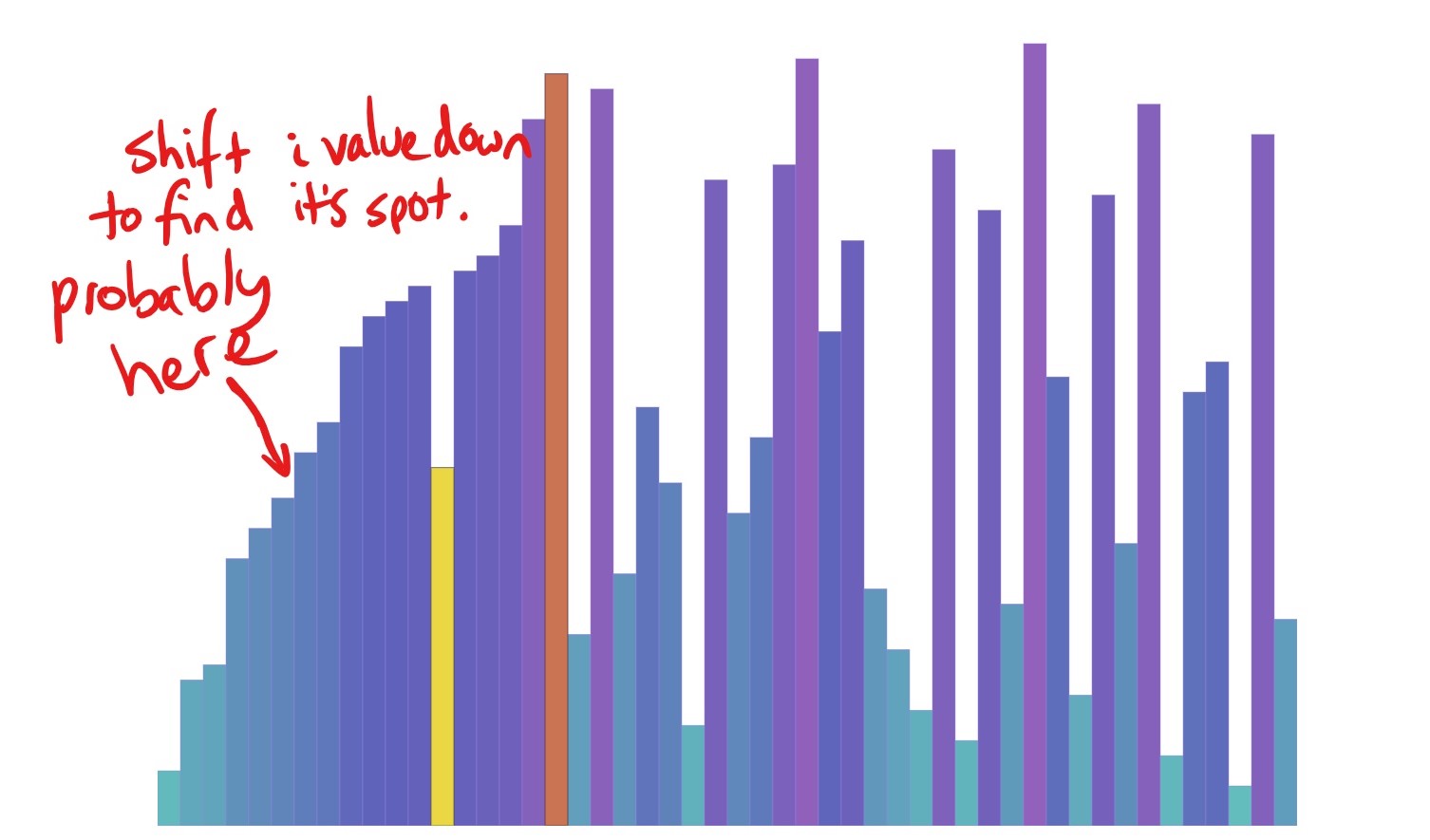
Halfway through sorting
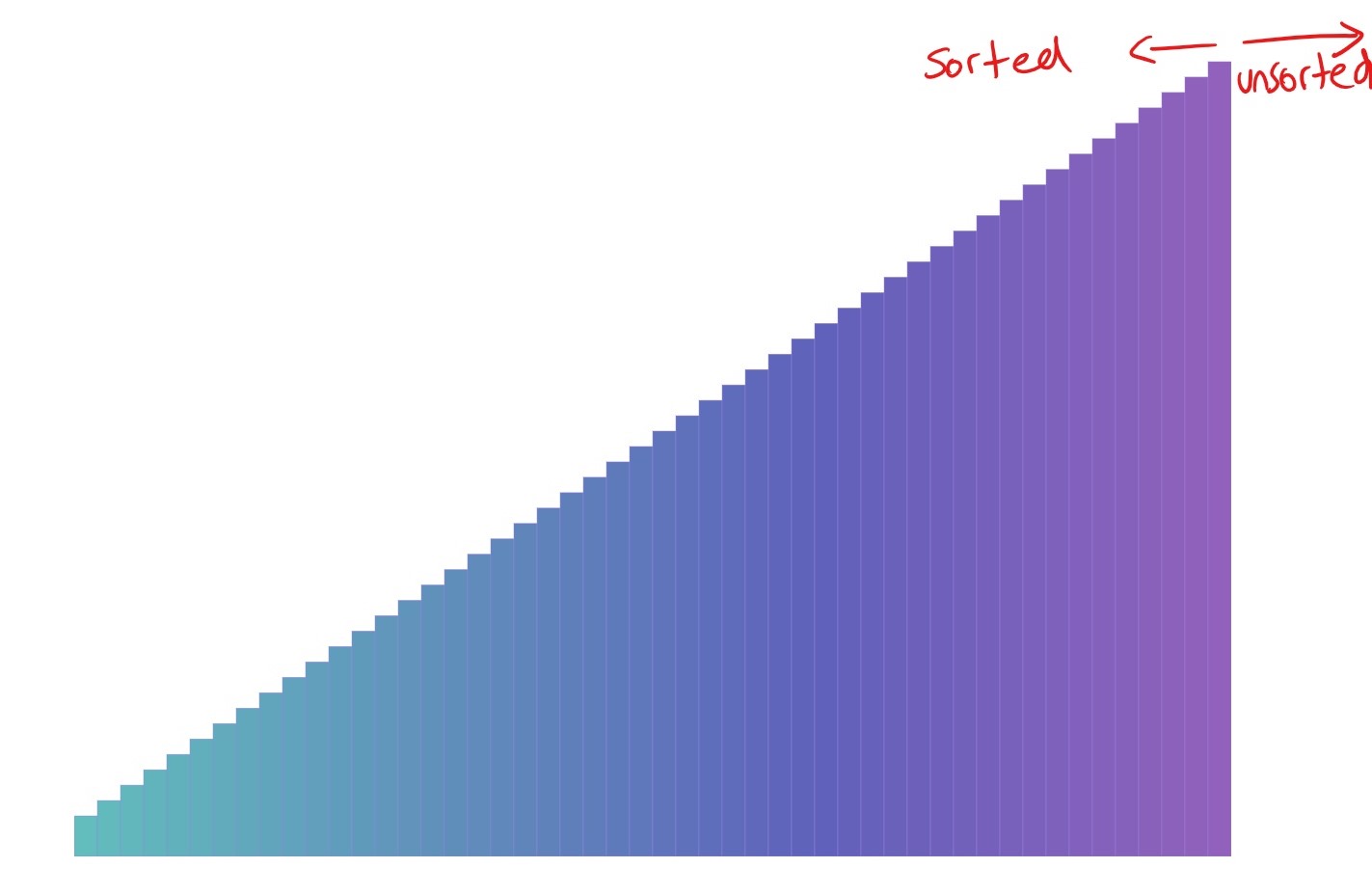
Finished sorting

This seemingly small bit of information is key to reasoning about the correctness of our algorithm!

Let’s take a look at a couple of other sorts very similar to insertion sort…

Bubble sort #

Bubble sort gets its name from the way it causes the biggest values to ‘bubble up’ to the top. It is executed by looping through the array, comparing two values at a time. If the first value is bigger than the second value, they need to be swapped. We continue to go through the array until no swaps have occurred.

The above visualisation is implemented with this code:

    function bubbleSort(arr) {
      let swaps = false;
      let count = 0;
      do {
        swaps = false;
        for (let i = 0; i < arr.length - count; i++) {
          if (arr[i] > arr[i + 1]) {
            const temp = arr[i];
            arr[i] = arr[i + 1];
            arr[i + 1] = temp;
            swaps = true;
          }
        }
        count += 1;
      } while (swaps);
      return arr;
    }

This version of bubble sort has been optimised slightly by reducing the inner loop length with each while loop. This is because we know that with each iteration, the biggest value will end up in its correct position. So we don’t need to loop over the last values. The count variable is responsible for keeping track of how many times we have completed our outer loop. Because we know that with each outer loop a new value moves to its final position, we can loop over one less value next time.

We are also keeping track of whether or not swaps happened. If no swaps occur, we know all our items are sorted. This means that if we are looping through an already sorted list, we only have to loop once! Try out the ‘Best case’ option from the dropdown to see this in action.

Our loop invariant for bubble sort is that we know all elements in the subarray $[n - i, …n]$are sorted (where $n$ is the length of our array). Let’s break this down into each of the loop invariant conditions:

This is a very similar reasoning to…

Selection sort #

Selection sort is on a very similar mission to bubble sort in that it also strives to create a sorted subarray. I like to think of it a little bit like a talent quest. With each new i pointer, we search the rest of the array for the smallest value and the smallest value we find will win that i spot. I’ve made it so the one below looks for the smallest value, but you could do one to search for all the biggest values instead (this also applies to bubble sort - ie you could push all the lowest values to the bottom rather than bubble the largest up to the top). The same loop invariant applies in both scenarios - you’re always going to be building that sorted subarray up from nothing.

This implements the following code:

  function selectionSort(arr) {
    for (let i = 0; i < arr.length; i++) {
      let smallestIndex = i;
      for (let j = i + 1; j < arr.length; j++) {
        if (arr[j] < arr[smallestIndex]) {
          smallestIndex = j;
        }
      }
      const temp = arr[i];
      arr[i] = arr[smallestIndex];
      arr[smallestIndex] = temp;
    }
    return arr;
  }

Each time we begin a loop we are hunting for the smallest value. When it first starts, it is looking for the smallest value in the $[1, …n]$ subarray to fill the 0th position. Once the first loop is finished, we know we have the smallest value in the slot for the smallest value (the 0 slot). We can then move onto the next slot. We then loop through the $[2, …n]$ subarray for the next smallest value which will be put in the 1 slot. By the time the outer loop has made it over the entire array, we know that each value has been purposefully selected and placed in it’s correct slot.

Efficiency comparison #

It’s important to understand the efficiency of the algorithms we write, so let’s take a look the efficiency of our algorithms above using big O notation.

Worst case scenario #

The worst case scenario (ie a list in reverse order) is the most important scenario to consider when thinking about efficiency. We want to write robust programs and that certainly won’t happen if we only ever consider the best possible scenario!

In the worst case, all 3 of the above algorithms have a time complexity of $O(n^2)$ or quadratic time.

This is because they all contain nested loops that are dependent on the size of the input array ($n$). This means they matter to the time complexity. The outer loop tells us to visit all elements in our list once (n times), but for each time we do this, we encounter another loop within it that tells us to loop over all the elements in our list again. So we end up visiting each element $n^2$ times.

All of our functions above include nested loops, so in the worst case scenario, they all have to loop $n^2$ times. But they do have different best case scenarios…

Best case scenario #

Although we should always characterise an algorithm’s efficiency based on the worst case scenario, the best case scenario can help us compare efficiencies between algorithms. For insertion sort and bubble sort, they both have a best case scenario of $O(n)$ or linear time, which is much better than quadratic time!

This is because:

Try restarting both the bubble sort and insertion sort simulations with the ‘Best case’ selected to see what this looks like.

Selection sort, however is different. Even in the best case scenario, it still has a time complexity of $n^2$.

This is because selection sort will always execute both loops no matter what. Values are not sorted by shifting around, but are purposefully placed into selected spots. And the logic of selection sort is that it must look through the entire array to ensure it finds the smallest value. It cannot say with certainty that the number is the smallest in the subarray unless it compares it to every other number in the subarray…. therefore looping $n^2$ times. See the difference when you turn on best case scenario for selection sort? Even though it is sorted, it has no knowledge of it!

Back to top